ICML Topological Deep Learning Challenge 2024: Beyond the Graph Domain

Welcome to the Topological Deep Learning Challenge 2024: Beyond the Graph Domain, jointly organized by TAG-DS & PyT-Team and hosted by the Geometry-grounded Representation Learning and Generative Modeling (GRaM) Workshop at ICML 2024.

See also

Link to the challenge repository: pyt-team/challenge-icml-2024.

Organizers, reviewers, and contributors: Guillermo Bernárdez, Lev Telyatnikov, Marco Montagna, Federica Baccini, Nina Miolane, Mathilde Papillon, Miquel Ferriol-Galmés, Mustafa Hajij, Theodore Papamarkou, Johan Mathe, Audun Myers, Scott Mahan, Olga Zaghen, Maria Sofia Bucarelli, Hansen Lillemark, Sharvaree Vadgama, Erik Bekkers, Tim Doster, Tegan Emerson, Henry Kvinge.

Winners

🏆 1st Category

🥇 1st-place, PR 63: Random Latent Clique Lifting (Graph to Simplicial); by Mauricio Tec, Claudio Battiloro, George Dasoulas

🥈 2nd-place, PR 58: Hypergraph Heat Kernel Lifting (Hypergraph to Simplicial); by Matt Piekenbrock

🥉 3rd-place, PR 11: DnD Lifting (Graph to Simplicial); by Jonas Verhellen

🏆 2nd Category

🥇 1st-place, PR 57: Simplicial Paths Lifting (Graph to Combinatorial); by Manuel Lecha, Andrea Cavallo, Claudio Battiloro

🥈 2nd-place, PR 32: Matroid Lifting (Graph to Combinatorial); by Giordan Escalona

🥉 3rd-place, PR 33: Forman-Ricci Curvature Coarse Geometry Lifting (Graph to Hypergraph); by Michael Banf, Dominik Filipiak, Max Schattauer, Liliya Imasheva

🏆 3rd Category

🥇 1st-place, PR 53: PointNet++ Lifting (Pointcloud to Hypergraph); by Julian Suk, Patryk Rygiel

🥈 2nd-place, PR 30: Kernel Lifting (Graph to Hypergraph); by Alexander Nikitin

🥉 3rd-place, PR 45: Mixture of Gaussians + MST Lifting (Pointcloud to Hypergraph); by Sebastian Mežnar, Boshko Koloski, Blaž Škrlj

🏆 4th Category

🥇 1st-place, PR 32: Matroid Lifting (Graph to Combinatorial); by Giordan Escalona

🥈 2nd-place, PR 33: Forman-Ricci Curvature Coarse Geometry Lifting (Graph to Hypergraph); by Michael Banf, Dominik Filipiak, Max Schattauer, Liliya Imasheva

🥉 3rd-place, PR 58: Hypergraph Heat Kernel Lifting (Hypergraph to Simplicial); by Matt Piekenbrock

🏆 Honorable Mentions

• ⭐ Great Contributors ⭐

  • Martin Carrasco (PRs 28, 29, 41, 50)

  • Bertran Miquel-Oliver, Manel Gil-Sorribes, Alexis Molina, Victor Guallar (PRs 14, 16, 21, 37, 42)

  • Theodore Long (PRs 22, 35, 65)

  • Jonas Verhellen (PRs 5, 7, 8, 10, 11)

  • Pavel Snopov (PRs 6, 9, 18, 20)

  • Julian Suk, Patryk Rygiel (PRs 23, 34, 53)

• 🎖️ Highlighted Submissions 🎖️

  • PR 49: Modularity Maximization Lifting (Graph to Hypergraph); by Valentina Sánchez

  • PR 47: Universal Strict Lifting (Hypergraph to Combinatorial); by Álvaro Martinez

  • PR 48: Mapper Lifting (Graph to Hypergraph); by Halley Fritze, Marissa Masden

Motivation

In the field of Topological Deep Learning (TDL), one of the primary objectives revolves around developing deep learning models tailored for data supported on topological domains, including simplicial complexes, cell complexes, and hypergraphs. These domains encapsulate diverse structures encountered in scientific computations. Naturally, topological domains serve as a means to represent higher-order interactions inherent in any complex system, such as social connections within communities, molecular structures and reactions, n-body interactions, among others. Specifically, TDL techniques facilitate the encoding of higher-order relationships utilizing algebraic topology principles; Fig. 1 illustrates the standard topological domains used to that end.

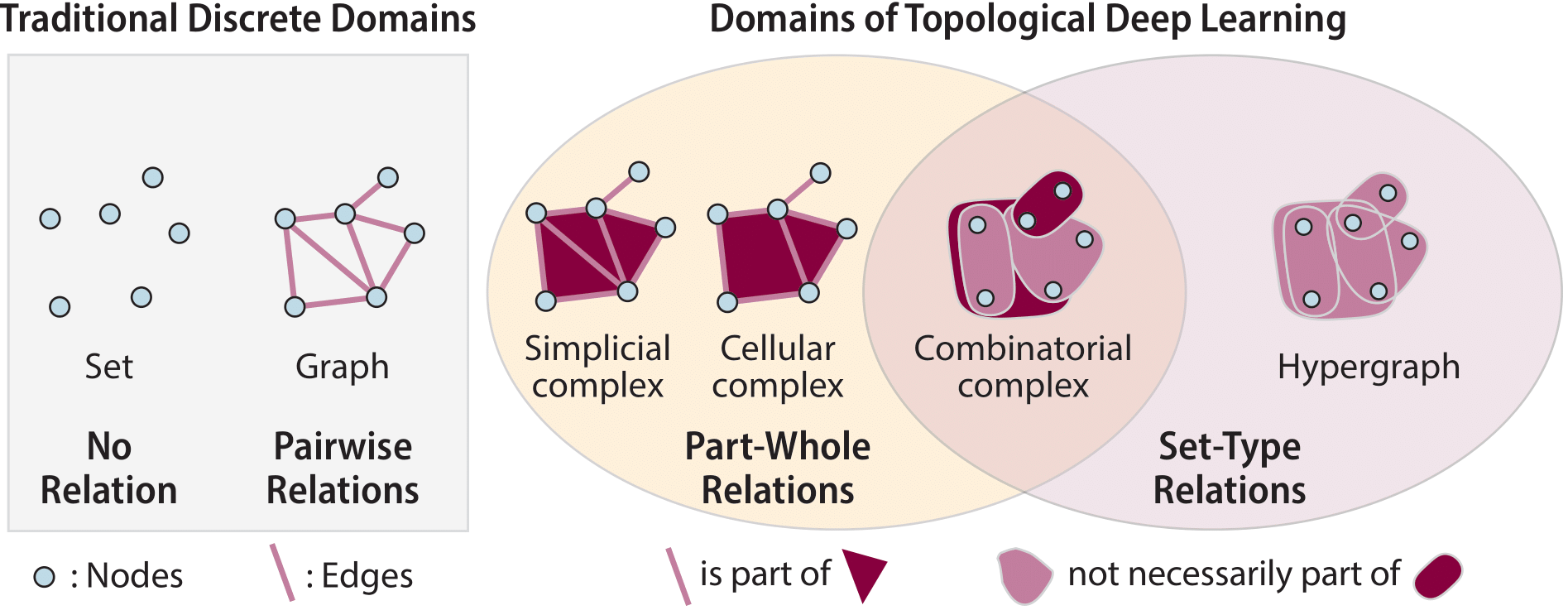
Fig. 1 Domains of Topological Deep Learning. Figure adopted from Hajij et al., 2023. (work highly recommended for those interested in knowing more details about these domains).

Despite its recent emergence, TDL is already postulated to become a relevant tool in many research areas and applications, from complex physical systems and signal processing to molecular analysis or social interactions, to name a few. However, a current limiting factor is that most existing datasets are presently stored as point clouds or graphs, i.e. the traditional discrete domains (Fig. 1). While researchers have introduced various mechanisms for extracting higher-order elements, it remains unclear how to optimize the process given a specific dataset and task.

The main purpose of this challenge is precisely to foster new research and knowledge about effective mappings between different topological domains and data structures, helping to expand the current scope and impact of TDL to a much broader range of contexts and scenarios.

Remark: This process of mapping a data structure to different topological domains is called “topological lifting”, or just “lifting” to abbreviate; Fig. 2 shows some visual examples. The “topological lifting” transfers data from the original domain where the signal (node/edge features) exists to the new domain where new objects can exist, such as simplicial/cell complexes. Therefore, it’s crucial to also derive and provide descriptors for these introduced objects, and this process is known as “feature lifting”.

Fig. 2 Examples of liftings: (a) A graph is lifted to a hypergraph by adding hyperedges that connect groups of nodes. (b) A graph can be lifted to a cellular complex by adding faces of any shape. (c) Hyperedges can be added to a cellular complex to lift the structure to a combinatorial complex. Figure adopted from Hajij et al. 2023.

Description of the Challenge

We propose that participants design and implement lifting mappings between different data structures and topological domains (point-clouds, graphs, hypergraphs, simplicial/cell/combinatorial complexes), to bridge the gap between TDL and all kinds of existing datasets.

In particular, participants can either implement already proposed liftings from the literature (see Related References section below), or design original approaches; both options are equally allowed. In the case of submissions with novel liftings, we emphasize that participants will keep all the credit for their implementations, and neither the challenge nor its related reward outcomes will prevent them from publishing their independent works.

Moreover, aligned with the primary goal of broadening the footprint and usage of TDL, the submission of liftings from point-clouds/graphs to higher-order topological domains is encouraged. However, this is not a requirement: the challenge also welcomes transformations between any other pair of topological structures (e.g., from hypergraph to simplicial domain).

In order to ensure consistency and compositionality, implementations need to be compatible with the BaseTransform class of torch_geometric, and should leverage NetworkX/TopoNetX/ TopoEmbedX libraries when dealing with graph/higher-order datasets. Each submission takes the form of a Pull Request to challenge-icml-2024 repo containing the necessary code for implementing a lifting map. More details are provided in subsequent sections below.

Note: We invite participants to review this webpage regularly, as more details might be added to answer relevant questions and doubts raised to the organizers.

Reward Outcomes [1]

⭐️ Every submission respecting the submission requirements will be included in a white paper summarizing the findings of the challenge, published in PMLR through the GRaM Workshop at ICML 2024. All participants with qualifying submissions will have the opportunity to co-author this publication.

📘 Winning participants will also have the opportunity to co-author a paper with an in-depth study on lifting procedures, focusing on assessing different transformations across topological domains. This work will be submitted to the Journal of Data-centric Machine Learning Research (DMLR).

🏆 Winner submissions will receive special recognition at ICML 2024 GRaM Workshop, where the Award Ceremony will take place.

Deadline

The final submission deadline is July 12th, 2024 (AoE). Participants are welcome to modify their Pull Request until this time.

Guidelines

Everyone can participate and participation is free –only principal PyT-Team developers are excluded. It is sufficient to:

• Send a valid Pull Request (i.e. passing all tests) before the deadline.

• Respect Submission Requirements (see below).

Teams are accepted, and there is no restriction on the number of team members. An acceptable Pull Request automatically subscribes a participant/team to the challenge.

We encourage participants to start submitting their Pull Request early on, as this helps addressing potential issues with the code. Moreover, earlier Pull Requests will be given priority consideration in the case of multiple submissions of similar quality implementing the same lifting.

A Pull Request should contain no more than one lifting. However, there is no restriction on the number of submissions (Pull Requests) per participant/team.

Submission Requirements

The submission must implement a valid lifting transformation between any pair of the following data structures: point-cloud/graph, hypergraph, simplicial complex, cell complex, and combinatorial complex. For a lifting to be valid, participants must implement a mapping between the topological structures of the considered domains –topology lifting. Participants may optionally implement a procedure to define the features over the resulting topology –feature lifting.

All submitted code must comply with the challenge’s GitHub Action workflow, successfully passing all tests, linting, and formatting (i.e., ruff). Moreover, to ensure consistency, we ask participants to use TopoNetX’s classes to manage simplicial/cell/combinatorial complexes whenever these topological domains are the target –i.e., destination– of the lifting.

Remark: We highly encourage the use of TopoNetX, TopoEmbedX and NetworkX libraries.

Topology Lifting (Required)

Submissions can implement already proposed liftings from the literature, as well as novel approaches. In the case of original liftings, we note that neither the challenge nor its related publications will prevent participants from publishing their own work: they will keep all the credit for their implementations.

For a lifting from a certain source domain src (e.g. graph) to a topological destination dst (e.g. simplicial), a submission consists of a Pull Request to the ICML Challenge repository that contains the following files:

1. {id lifting}_lifting.py (e.g. clique_lifting.py)

   • Stored in the directory modules/transforms/liftings/{src}2{dst}/

   • Defines a class {Id lifting}Lifting that implements a lift_topology() method that performs the specific {src}2{dst} topological lifting considered (e.g.

     SimplicialCliqueLifting as a graph2simplicial transform). It may also implement other auxiliary functions, and can override parent methods if required.
   • This class must inherit from {Src}2{Dst}Lifting abstract class (e.g.

     Graph2SimplicialLifting), which we provide for every pair {src,dst} within the corresponding directory. When justified, this and other abstract parent classes can be modified.

   • The implemented lifting –and in general, any implemented data/feature transformation– must be added to TRANSFORMS dictionary in data_transform.py file, located at modules/transforms/ directory. The keys of ‘TRANSFORMS’ dictionary correspond to ‘transform_name’ field in corresponding .yaml files while the values refers to corresponding class that implements the logic of the transform.

   Note: We provide several lifting examples for graph2simplicial, graph2cell and

   graph2hypergraph.

2. {id lifting}_lifting.yaml (e.g. clique_lifting.yaml)

   • Stored in the directory configs/transforms/liftings/{src}2{dst}/

   • Defines the default parameters of the implemented transform.

   Note: You can find config examples for all our implemented liftings and data transforms.

3. {id lifting}_lifting.ipynb (e.g. clique_lifting.py)

   • Stored in the directory tutorials/{src}2{dst}/

   • Contains the following steps:

     1. Dataset Loading

        • Implements the pipeline to load a dataset from the src domain. Since the challenge repository doesn’t allow storing large files, loaders must download datasets from external sources into the datasets/ folder.

        • This pipeline is provided for several graph-based datasets. For any other src domain, participants are allowed to transform graph datasets into the corresponding domain through our provided lifting mappings –or just dropping their connectivity to get point-clouds.

        • (Bonus) Designing a loader for a new dataset (ones that are not already provided in the tutorials) will be positively taken into consideration in the final evaluation.

     2. Pre-processing the Dataset

        • Applies the lifting transform to the dataset.

        • Needs to be done through the PreProcessor, which we provide in

          modules/io/preprocess/preprocessor.py.

     3. Running a Model over the Lifted Dataset

        • Creates a Neural Network model that operates over the dst domain, leveraging TopoModelX for higher order topologies or torch_geometric for graphs.

        • Runs the model on the lifted dataset.

   Note: Several examples are provided in tutorials/.

4. test_{id lifting}.py (e.g. test_cycle_lifting.py)

   • Stored in the directory tests/transforms/liftings/{src}2{dst}/

   • Contains one class, Test{Id lifting}, which contains unit tests for all of the methods contained in the {Id lifting}Lifting class.

   • Please use pytest (not unittest).

   Note: We provide several examples in the corresponding directories.

Feature Lifting (Optional)

Some TDL models require well-defined features on higher-order structures (e.g. 2-cells, or hyperedges); therefore, in their more general formulation, liftings also need to produce initial features for every topological element of the dst domain. In particular, in all our examples we make use of a straightforward SumProjection transform to that end, which gets the desired structural features by sequentially projecting the original signals via incidence matrices.

Participants are more than welcome to implement new feature liftings mappings, which can be added to the feature_liftings.py file at the modules/transforms/feature_liftings/ directory. However, we remark this is optional, and it will only be regarded as a bonus.

Note: Please, reach out if you want to know more details about how to implement a new feature lifting and/or a novel data loader. We also provide some data manipulations transforms that could be useful when defining more complex data pipelines.

Evaluation

Award Categories

Given the lack of an exhaustive analysis about different types of procedures to infer the topological structure within TDL, there is not any particular requirement for submitted liftings –apart from a high-quality code implementation. To promote and guide diversity in submissions, we propose the following general, non-mutually exclusive award categories:

• Best implementation of a existing lifting from the literature.

• Best novel lifting design that only leverages the relational information of the source domain (i.e. connectivity-based lifting).

• Best novel lifting design that leverages the original features of the source domain to infer the target topology (i.e. feature-based lifting). If available, connectivity can also be simultaneously used.

• Best implementation of a deterministic lifting (existing or novel).

• Best implementation of a non-deterministic lifting (existing or novel).

We encourage participants to tag and categorize their Pull Requests with these and other possible taxonomies. In fact, we might reconsider some categories based on participants feedback and submissions. Additionally, we reserve the right to award some honorable mentions considering some aspects like originality, theoretical robustness, loading interesting datasets, implementing new feature liftings, etc.

Evaluation Procedure

The Condorcet method will be used to rank the submissions and decide on the winners in each category. The evaluation criteria will be:

• Does the submission implement the lifting correctly? Is it reasonable and well-defined?

• How readable/clean is the implementation? How well does the submission respect the submission requirements?

• Is the submission well-written? Do the docstrings clearly explain the methods? Are the unit tests robust?

Note that these criteria do not reward final model performance, nor the complexity of the method. Rather, the goal is to implement well-written and accurate liftings that will unlock further experimental evidence and insights in this field.

Selected PyT-Team maintainers and collaborators, as well as each team whose submission(s) respect(s) the guidelines, will vote once on Google Form to express their preference for the best submission in each category. Note that each team gets only one vote/domain, even if there are several participants in the team.

A link to a Google Form will be provided to record the votes. While the form will ask for an email address to identify the voter, voters’ identities will remain secret–only the final ranking will be shared.

Questions

Feel free to contact us through GitHub issues on this repository, or through the Geometry and Topology in Machine Learning slack. Alternatively, you can contact us via mail at any of these accounts: guillermo.bernardez@upc.edu, lev.telyatnikov@uniroma1.it.

Related References

As a support to participants, in this section we share some related references that propose topological liftings or might help defining novel ones.

1. Papillon, M., Sanborn, S., Hajij, M., & Miolane, N. (2023). Architectures of Topological Deep Learning: A Survey on Topological Neural Networks. arXiv preprint arXiv:2304.10031.

2. Hajij, M., Zamzmi, G., Papamarkou, T., Miolane, N., Guzmán-Sáenz, A., Ramamurthy, K. N., et al. (2022). Topological deep learning: Going beyond graph data. arXiv preprint arXiv:2206.00606.

3. Baccini, F., Geraci, F., & Bianconi, G. (2022). Weighted simplicial complexes and their representation power of higher-order network data and topology. Physical Review E, 106(3), 034319.

4. Barbarossa, S., & Sardellitti, S. (2020). Topological signal processing over simplicial complexes. IEEE Transactions on Signal Processing, 68, 2992–3007.

5. Battiloro, C., Spinelli, I., Telyatnikov, L., Bronstein, M., Scardapane, S., & Di Lorenzo, P. (2023). From latent graph to latent topology inference: differentiable cell complex module. arXiv preprint arXiv:2305.16174.

6. Benson, A. R., Gleich, D. F., & Higham, D. J. (2021). Higher-order network analysis takes off, fueled by classical ideas and new data. arXiv preprint arXiv:2103.05031.

7. Bodnar, C., Frasca, F., Otter, N., Wang, Y., Lio, P., Montufar, G. F., & Bronstein, M. (2021). Weisfeiler and Lehman go cellular: Cw networks. In Advances in neural information processing systems (Vol. 34, pp. 2625–2640).

8. Bodnar, C., Frasca, F., Wang, Y., Otter, N., Montufar, G. F., Lio, P., & Bronstein, M. (2021, July). Weisfeiler and Lehman go topological: Message passing simplicial networks. In International Conference on Machine Learning (pp. 1026-1037). PMLR.

9. Elshakhs, Y. S., Deliparaschos, K. M., Charalambous, T., Oliva, G., & Zolotas, A. (2024). A Comprehensive Survey on Delaunay Triangulation: Applications, Algorithms, and Implementations Over CPUs, GPUs, and FPGAs. IEEE Access.

10. Ferri, M., Bergomi, D. M. G., & Zu, L. (2018). Simplicial complexes from graphs towards graph persistence. arXiv preprint arXiv:1805.10716.

11. Gao, Y., Zhang, Z., Lin, H., Zhao, X., Du, S., & Zou, C. (2020). Hypergraph learning: Methods and practices. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(5), 2548–2566.

12. Hajij, M., & Istvan, K. (2021). Topological deep learning: Classification neural networks. arXiv preprint arXiv:2102.08354.

13. Hajij, M., Zamzmi, G., Papamarkou, T., Miolane, N., Guzmán-Sáenz, A., & Ramamurthy, K. N. (2022). Higher-order attention networks. arXiv preprint arXiv:2206.00606, 2(3), 4.

14. Hajij, M., Zamzmi, G., Papamarkou, T., Guzman-Saenz, A., Birdal, T., & Schaub, M. T. (2023). Combinatorial complexes: bridging the gap between cell complexes and hypergraphs. In 2023 57th Asilomar Conference on Signals, Systems, and Computers (pp. 799–803). IEEE.

15. Hoppe, J., & Schaub, M. T. (2024). Representing Edge Flows on Graphs via Sparse Cell Complexes. In Learning on Graphs Conference (pp. 1-1). PMLR.

16. Jogl, F., Thiessen, M., & Gärtner, T. (2022). Reducing learning on cell complexes to graphs. In ICLR 2022 Workshop on Geometrical and Topological Representation Learning.

17. Kahle, M. (2007). The neighborhood complex of a random graph. Journal of Combinatorial Theory, Series A, 114(2), 380–387.

18. Kahle, M., & others. (2014). Topology of random simplicial complexes: a survey. AMS Contemp. Math, 620, 201–222.

19. Kahle, M. (2016). Random simplicial complexes. arXiv preprint arXiv:1607.07069.

20. Liu, X., & Zhao, C. (2023). Eigenvector centrality in simplicial complexes of hypergraphs. Chaos: An Interdisciplinary Journal of Nonlinear Science, 33(9).

21. Lucas, M., Gallo, L., Ghavasieh, A., Battiston, F., & De Domenico, M. (2024). Functional reducibility of higher-order networks. arXiv preprint arXiv:2404.08547.

22. Ruggeri, N., Battiston, F., & De Bacco, C. (2024). Framework to generate hypergraphs with community structure. Physical Review E, 109(3), 034309.

[1]

By law, US researchers are not allowed to co-author papers with scholars from some countries and institutions. Participants are responsible for checking eligibility.